I've always liked Conway's Game of Life since I first saw it, it's really cool to see how a reasonably small set of rules can lead to such complexity and 'life-like' patterns.
Conway's Game of Life is played on an grid where each cell is either alive or dead. Once the initial state is set at generation 0 with some cells alive and others dead the status of the cells in the next generation are determined based on their current status and the status of the immediately adjacent 8 neighbors (including diagonals). For the next generation the following transitions occur:
This set of rules, as originally described by John Conway in 1970 can lead to some really interesting, and exciting, patterns. For example here is a game which starts from just a few set cells:
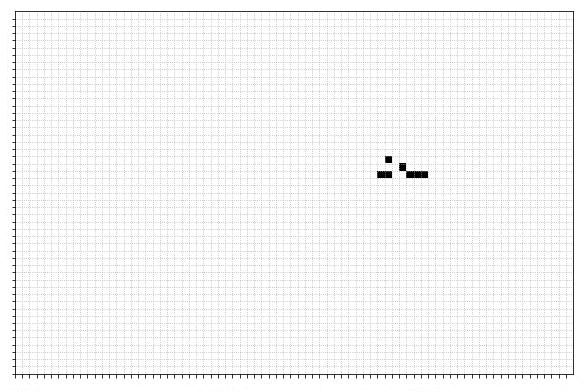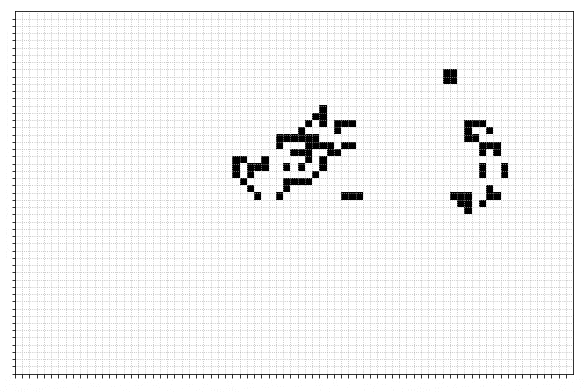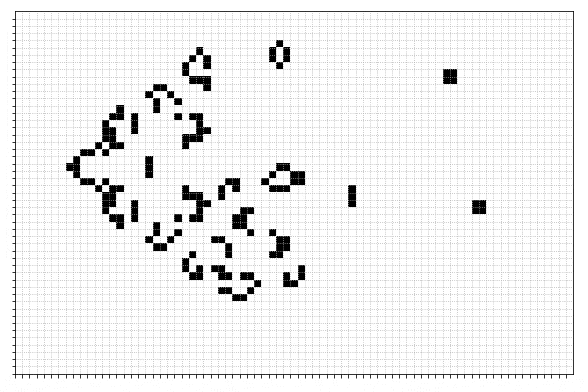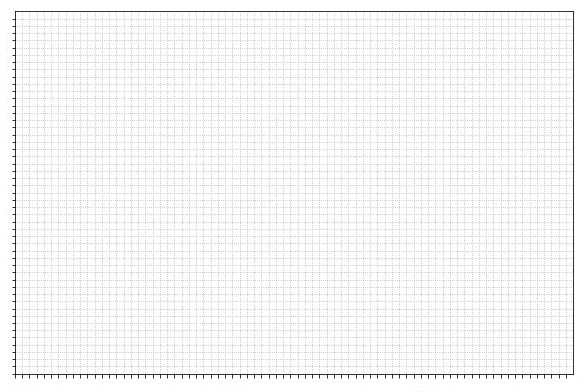
But what if we wanted to pick some 'ending' configuration and find some initial arrangement of living and dead cells that evolve towards that configuration in the future? Or if we wanted to take individual steps backwards?
Unfortunately there is no direct way to apply the rules described above in reverse. Also, the brute force method of enumerating different starting configurations and stepping them forwards to check really doesn't scale very well.
One technique, described by Donald Knuth in 'The Art of Computer Programming' Volume 4 Fascicle 6, is based on boolean satisfiability. I will not describe the technique in too much detail here. The point I want to make on this page is about encoding sophistication and performance.
The bare bones description I can give of this technique is that boolean satisfiability works with extraordinarily simple building blocks. A set of variables which can be either true or false, and a set of clauses which describe some necessary restrictions on those variables.
So for example, if I had two boolean variables say x and y then there are four different satisfying assignments of true and false to these variables. I could then start adding some clauses or restrictions, like for example: (x ∨ y). Now there are only three assignments that satisfy. The ∨ symbol means 'or'. so the above clause says that either x or y must be true.
Back to the game of life, we can define boolean variables for each grid cell for each time period with true meaning the cell is alive, and false meaning the cell is dead. Then we can add clauses that enforce the game of life. Knuth gives two different encodings with vastly different levels of sophistication.
The first encoding is naïve, and generates a ton of clauses with a lot of redundant information. Essentially, for each cell we generate a full set of 256 clauses, one for each different possible state of the cells 8 neighbors to enforce the state of the cell in the next time step.
The second encoding employs a hierarchical approach including extra variables which greatly reduces the number of clauses and describes a much more elegant and sophisticated encoding. However, surprisingly this sophisticated encoding actually performs much worse!
I implemented both of these encodings and used the fantastic Glucose sat solver to solve several instances and the straightforward naïve approach was more performant.
In my work I spend a lot of time coming up with different encodings for different problems in different mathematical contexts. In optimization there are always multiple ways to formulate a problem and in boolean satisfiability there are always these different encodings that crop up. The point is sometimes sophisticated techniques that sound a lot cooler and use a lot more elegant mathematical machinery might in the end be worse.
Of course this doesn't mean you should forego trying the sophisticated techniques. There's always value in trying something new because hey it might be better and if not at least you'll know that the first approach was better. But eh, just more weight on trying different approaches and not getting hung up on the one that sounds cooler because well, it might actually be a lot slower.
Anyway, here's one end result - I paused slightly on the relevant time step.
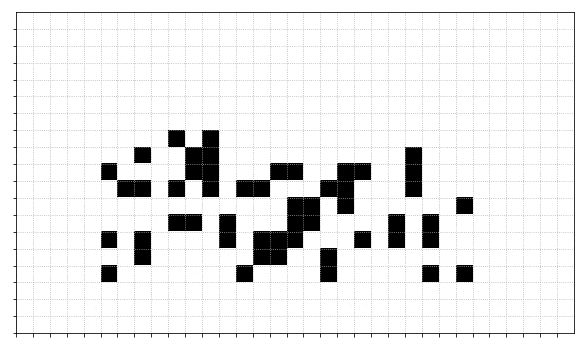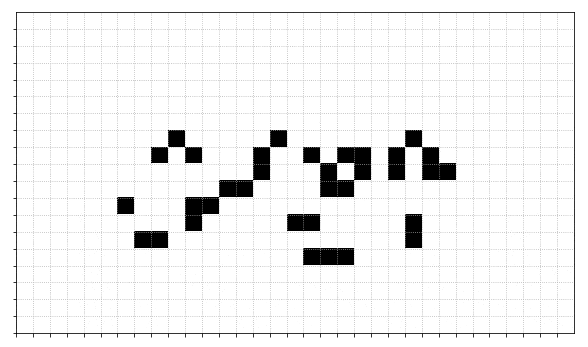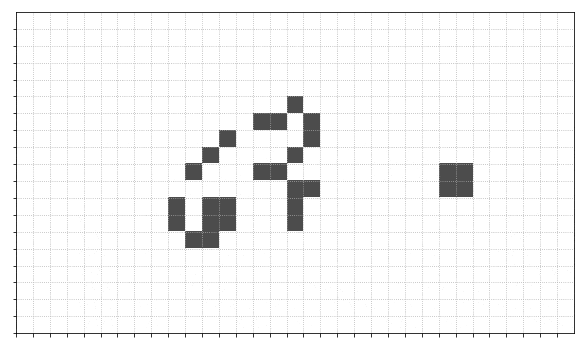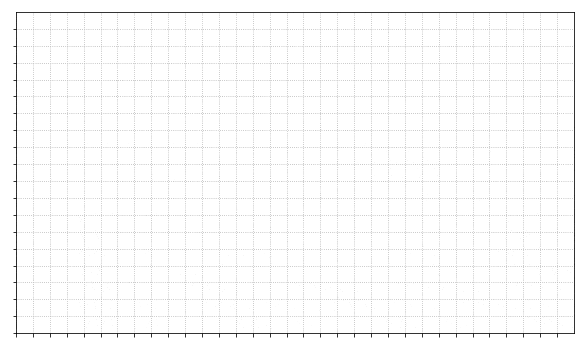
matthewvdeutsch@gmail.com - © Matthew Deutsch. All rights reserved.