| TITLE | Solving the Game of Ur | MM 19-1922-0 |
|---|---|---|
| AUTHOR— M.V. Deutsch | ||
| DATE— March 10, 2019 |
| FILING SUBJECTS— | Personal Project |
|---|---|
| Game of Ur |
The Royal Game of Ur is an ancient, two-player, stochastic, strategy board game. It’s simple, by modern standards, but it’s still very fun and worth your time. In this memo I present some sketches towards solving it for all positions, accounting for the probabilistic nature of the dice.
1 Introduction
The Royal Game of Ur is an ancient, two-player, stochastic, strategy board game that was likely first played during the early third millennium BC. It is a notable game, not only for its age and historical significance, but also because it is exciting and fun to play. It combines elements of both strategy and luck which make it a good subject for a rigorous mathematical treatment. I personally enjoy this game very much.
It is not so difficult as some of its descendants, such as backgammon, and the amount of strategy required, is not so overbearing as in chess or go. But more importantly the Royal Game of Ur is not mind numbing like ‘Snakes and Ladders’ or ‘Candyland’ or some of the other “games” that children and their unfortunate parents are often subjected to.
The Royal Game of Ur board was first discovered by Sir Leonard Woolley during his excavations of the Royal Cemetery of Ur between 1922 and 1934, but for many years it was unclear how to play the game. However, a cuneiform clay tablet by the ancient Babylonian scribe Itti-Marduk-Balāṭu was translated by the British Museum curator Irving Finkel and he was able to reconstruct the rules (Finkel 2007). The circumstances of the translation and reconstruction are very interesting, but unfortunately a bit off topic for this discussion.
My own interest in the game was prompted by a video produced by the British Museum wherein some of the history is explained and the game is played Youtube Link. I have since constructed my own board and have played the game with many people, including my kids who seem to take some perverse pleasure in beating me at it. This personal project is to explore the game itself in detail, and to ‘solve’ the game. In the same sense that checkers has been solved, in that for every possibly position the optimal move is known, and the probability of winning is also known.
The Royal Game of Ur is played on a board as shown below. Each player has seven checkers which originally start off the board. All seven of those checkers must progress through the entire board (14 squares) and then come of the board. Each player has their own A-D and M-N squares, and the middle E-L squares are shared.
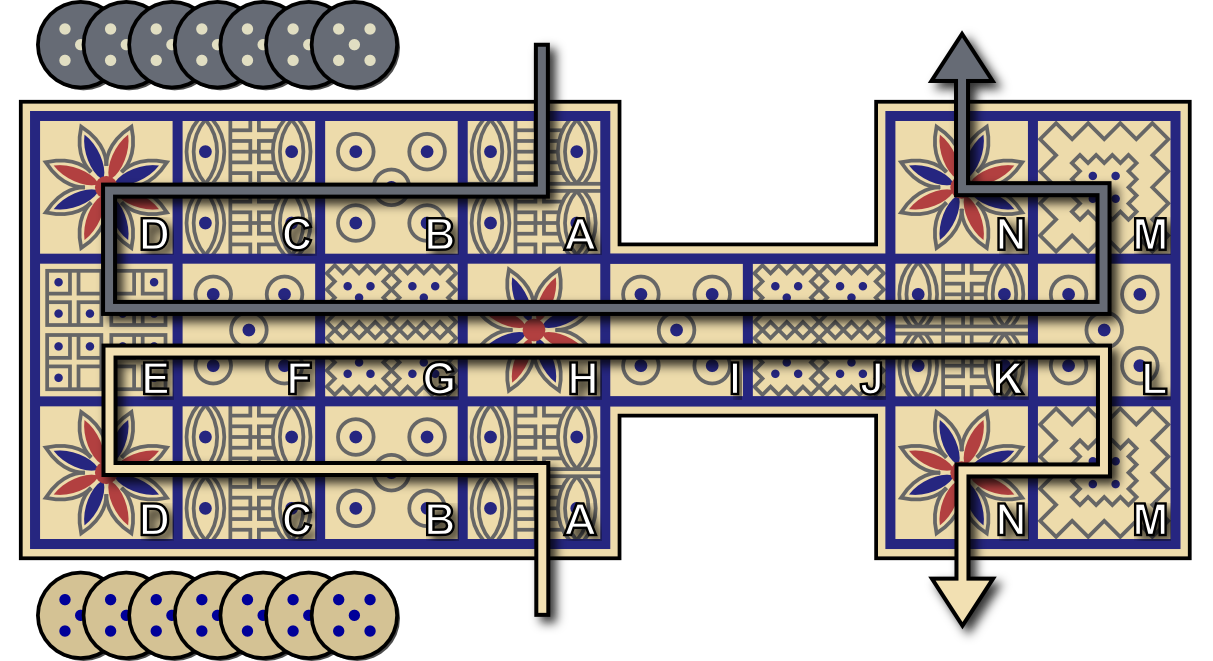
At the start of each turn, the player whose turn it is rolls four tetrahedral dice each with two corners marked and counts the number of showing marked corners. This is the amount that the player must move one of their checkers - either by coming on to the board, moving one already on the board, or coming off. If there are no legal moves than the turn is forfeit. In order to come off the board the amount must be rolled exactly. That is, to come off from N the player must roll a one.
On the shared squares E-G, and I-L, the checkers are not ‘safe’, and if they are landed on by an opponent checker they are returned off the board and must start over from the beginning. Squares D, H, and N, are special ‘rosette’ squares, and if landed on allow the player to roll again possibly making another decision. Note that a checker on the H square, a rosette, is safe from being landed on.
The game is over when the first player comes off with all seven of their checkers.
2 State of the game
The single most important aspect of the Royal Game of Ur that makes it even feasible to solve completely is the small state space and the low branching factor. The Royal Game of Ur is relatively simple. The complexity of several games is summarized in Table 1. There are, perhaps, more meaningful ways of classifying the complexity of a game - but this will serve to provide a order of magnitude comparison.
| Game | Number of Board Positions |
Average Branching Factor |
|---|---|---|
| Go (Baduk) | \(10^{173}\) | 250 |
| Chess | \(10^{43}\) | 35 |
| Checkers | \(10^{20}\) | 2.8 |
| Backgammon | \(10^{20}\) | 250 |
| Game of Ur | \(10^{8}\) | 3.3 |
The Royal Game of Ur consists of 20 squares, 12 of those are binary (1 checker or not), and 8 of them are trinary (white checker, black checker, or no checker). This gives an upper bound, ignoring the limit of seven checkers each, of \(2^{12} \times 3^8 = 26,873,856\) different possible positions. Through exhaustive enumeration there are \(18,746,644\) states with 0-7 checkers on the board for each player. But we must count the number of checkers each player has off as distinct to give \(137,913,936\) different game states. Again, though, we should really consider each possible roll of the die (of which there are 5), as distinct to get a final number of game states, including duplicate winning states, of \(689,569,680\).
The average branching factor was then calculated by brute force. I have summarized the different game states and the number of options available at each stage below.
| Number of Choices | Number of Game States |
|---|---|
| 0 | 139,711,089 |
| 1 | 23,479,368 |
| 2 | 103,188,832 |
| 3 | 195,500,624 |
| 4 | 162,791,787 |
| 5 | 56,992,374 |
| 6 | 7,473,143 |
| 7 | 257,107 |
One interesting implementation note is that I use a very space efficient encoding of the game state (not including the state of the dice) into a single 32 bit integer. This allows for a valid unique identifier of each position that is much easier to pass around than the standard `Forsyth-Edwards Notation’ in Chess for example.
The 32 bit integer is defined with the first 13 bits encoding the state of the shared E-L squares in a standard trinary to binary encoding. \(2^13\) is just greater than \(3^8\) so it fits. The next 12 bits encode the state of white’s and black’s six personal squares. Followed by 3 bits each for the number of checkers that are off the board for white and black. This leaves 1 last bit which I use to store the player’s turn.
3 Solving with One Checker
Unlike many problems in life, solving a game is typically started at
the end. In the case when both players have bore off six checkers each
they only have one left and the game reduces to something akin to snakes
and ladders (gross), where you’re just alternating rolling the dice and
seeing who rolls the right numbers first. This position, using my 32 bit
encoding, is position 1811939328. This section of the game
can be solved by setting up a Markov chain and using the fundamental
matrix.
First a side note on the dice. As I mentioned earlier the game does not use typical modern dice. Instead the Royal Game of Ur is played with 4 binary dice, where the results are summed to give the final move distance. Archaeologists have found two different types of dice near the boards, either 4 tetrahedrons with 2 corners marked, as in the Figure below, or as flat sticks with one side marked.

The player picks up the dice (actually a bit tricky with 4 tetrahedrons) and rolls them before adding the number of marked points together. This gives a non uniform distribution of possible rolls. As summarized below
| Roll | Probability | Percent |
|---|---|---|
| 0 | 1/16 | 6.25% |
| 1 | 1/4 | 25.0% |
| 2 | 3/8 | 37.5% |
| 3 | 1/4 | 25.0% |
| 4 | 1/16 | 6.25% |
With the state of the game understood, and these probabilities in
hand, it is reasonably straightforward to set up the complete transition
matrix starting from position 1811939328. We construct the
transition matrix \(P\) as the
following:
\[ P = \begin{bmatrix} Q & \overrightarrow{w} & \overrightarrow{b} \\ \overrightarrow{0}^T & 1 & 0 \\ \overrightarrow{0}^T & 0 & 1 \\ \end{bmatrix} \]
Where \(q_{ij}\) contains the transition probability from state \(i\) to state \(j\). \(w_i\) contains the probability of white winning from state \(i\), and \(b_i\) similarly contains the probability of black wining from state \(i\). Once we enter the winning state, either for white or black, we cannot leave. This is an absorbing Markov chain.
To solve for the probability of winning from any position take some powers of the transition matrix, and notice the pattern:
\[ P^2 = \begin{bmatrix} Q^2 & \overrightarrow{w} + Q \overrightarrow{w} & \overrightarrow{b} + Q \overrightarrow{b} \\ \overrightarrow{0}^T & 1 & 0 \\ \overrightarrow{0}^T & 0 & 1 \\ \end{bmatrix} \]
\[ P^3 = \begin{bmatrix} Q^3 & \overrightarrow{w} + Q \overrightarrow{w} + Q^2 \overrightarrow{w}^2 & \overrightarrow{b} + Q \overrightarrow{b} + Q^2 \overrightarrow{b} \\ \overrightarrow{0}^T & 1 & 0 \\ \overrightarrow{0}^T & 0 & 1 \\ \end{bmatrix} \]
\[ P^n = \begin{bmatrix} Q^n & (I + Q + Q^2 + ... + Q^{n-1}) \overrightarrow{w} & (I + Q + Q^2 + ... + Q^{n-1}) \overrightarrow{b} \\ \overrightarrow{0}^T & 1 & 0 \\ \overrightarrow{0}^T & 0 & 1 \\ \end{bmatrix} \]
But we know that \(Q^n \rightarrow 0\) as \(n \rightarrow \infty\) because \(\left\Vert Q \right\Vert < 1\). And then this is just the geometric series of matrices and \(I + Q + Q^2 + ... + Q^{n-1} = (I - Q)^{-1}\). We can then solve:
\[ (I - Q) \overrightarrow{x} = \overrightarrow{w} \]
This gives us the probability of winning, as white, (and black), from any position precisely. For example, in the beginning with both checkers off the board white (who gets to go first) has a 3% advantage because it is his turn. As a side note, I solved for these precisely with arbitrary precision rational numbers, and the true probability of winning as white from that initial position is:
\[ \overrightarrow{x}_0 = \frac{243768361614875553917696493...560745517481128246827646929}{459897057667994595135906789...073982544243335723876953125} \]
Where the top and bottom numbers are 227 digit numbers! This result motivated me to drop my notions of solving all the way up to 7 checkers with exact arithmetic, and does require me to look into the accuracy with respect to floating point arithmetic and this problem in particular. That is a future problem.
An interesting note is that there are three different ways of filling in the entries of the transition matrix; we could use a single roll of the dice, a players complete turn, or a players turn and the opponents response. The size of the transition matrix decreases if we do not treat positions where it is black’s turn as distinct, and the density of the matrix increases as we consider more events in a single transition.
These three different methods can be seen below. To be frank, this doesn’t make much of a difference with a transition matrix this small. We can solve for the final transition probabilities directly in less than a second regardless of how it is constructed. However this could be relevant when we consider more checkers.
4 Solving with Two Checkers
This work is currently on hold, but I would like to continue exploring dynamic programming techniques such as value / policy iteration, back tracing, bellmans optimality equations, and so much more. This is an extremely rich subject I just need to devote some more time to it to finish this off.