Origami is one of my favorite hobbies, it's nice to create something in the physical world instead of writing some code which you can't pick up and hold. It's nice to spend time on something and see it completed.
Normally origami is done with a single square of paper; no cuts, no glue. However these kinds of restrictions are made to be broken - which can lead to better art!
Modular origami is a branch of origami where the final model is made up of smaller units each folded from an individual piece of paper. The individual pieces of paper are often square, but not always. There are many different kind of units, some are custom to a particular model, and others can be used for many different models. The Sonobe unit and the PHiZZ unit (pentagon-hexagon zig-zag unit) are two versatile units which can be used to make many different models.
I made this torus from 360 PHiZZ units. It was a slog, to be honest! But I really like the final result. Huge thanks to my wife for taking the above picture - she makes it look so much better than it actually looks.
The PHiZZ unit is a simple unit for modular origami, which makes it ideal for larger models such as the torus. When you are folding 360 of something, it helps if they are relatively easy to do! The PHiZZ unit was originally created by Tom Hull . He originally used them to construct dodecahedrons, and other shapes such as buckyballs.
A single PHiZZ unit is only a couple of folds. Here are some diagrams:
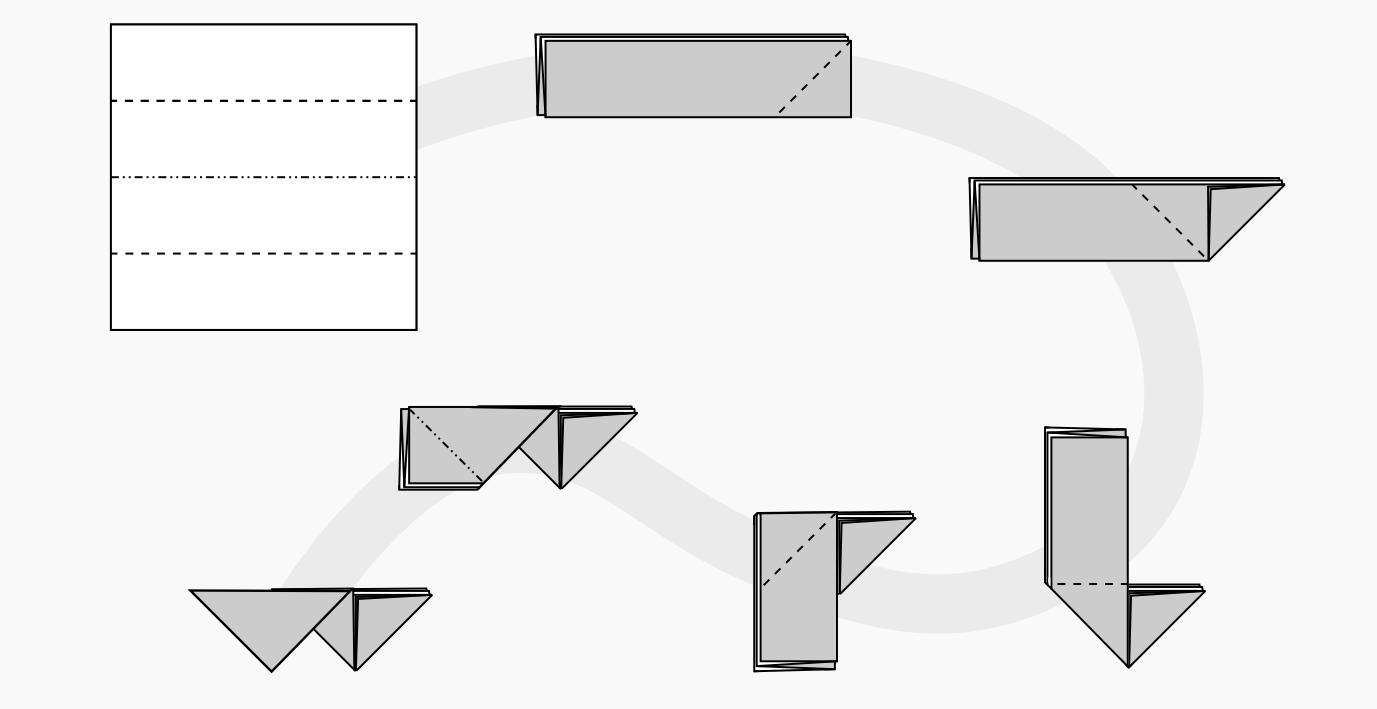
Three PHiZZ units are joined to create a pyramid, then additional pyramids can be formed from the other ends. You can create loops from the pyramids; To construct a dodecahedron use 30 units and make each loop consist of five edges.
For the torus, I needed 360 units. I did not come up with the idea in the first place - I saw a picture of another Torus and wanted one for myself. I'm not sure which torus I saw first or where I saw it, but when I was starting this project I searched for more information and found this website with some good instructions and recommendations: [mattersofgrey]. Unfortunately this link has since stopped working.
At the bottom of this page I included a schematic which would have helped me a bit more than the schematic at the above website. I was able to do it with their schematic - but I had a little trouble. I used paper that was about 3 inches square, and ended with a torus that was about 16 inches in diameter. Also, if you want to make your own torus I have a few of my own recommendations:
There are a couple really nice color schemes out there for this model, it certainly looks elegant in a single color. I've also seen a rainbow pattern which looks really cool. I wanted something a little bit bit different to go with the elefantenhaut paper I wanted to use, so I set out to find a three coloring.
The graph which is formed by the individual PHiZZ units is a 3-regular graph, in that each vertex has exactly 3 edges leaving it, so we know that it can be edge colored in at most 4 colors. To find the 3 coloring I folded a test one (yeah, an entire test torus out of just regular printer paper..), labeled the vertices / edges, and worked out the graph on a sheet of paper.
I used the fact that the graph has 12 fold rotational symmetry and I encoded 1 / 12 of the three coloring as a SAT problem and solved it with glucose. There are more efficient ways of solving three colorings, but this was fun. Luckily the torus graph is not a snark.
Oh yeah, I also made a quick visualization of the graph:
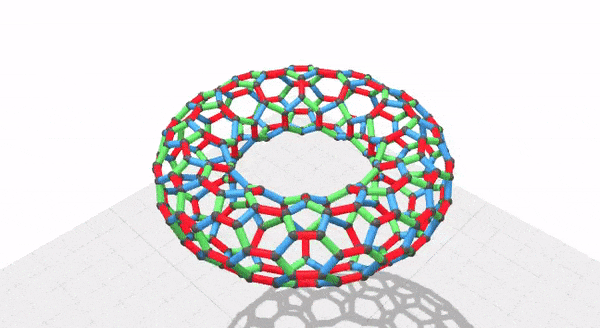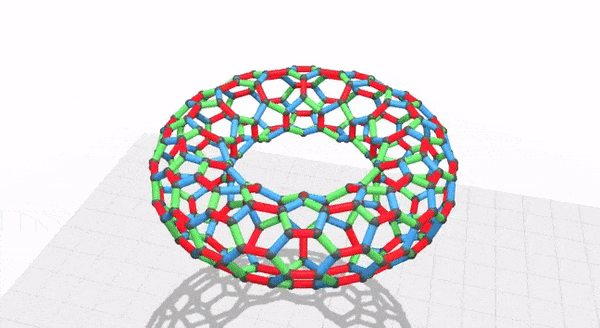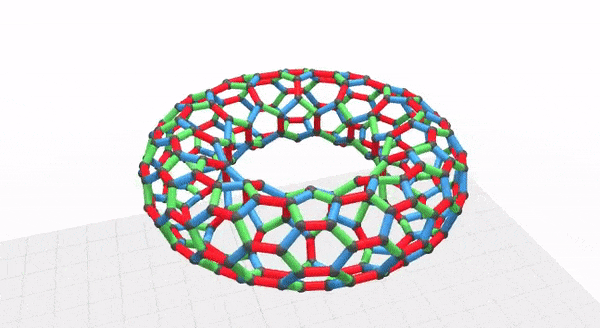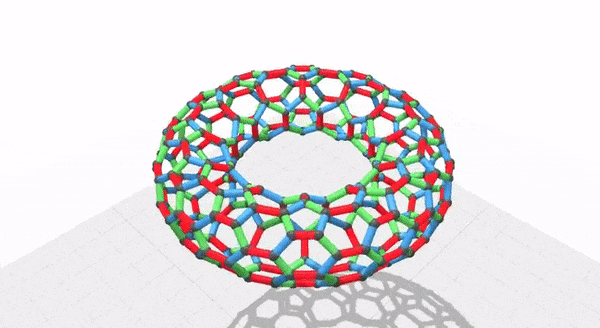
I used Zanders Elefantenhaut which is a book binding paper. It is relatively thick for origami but is really good for wetfolding, tesselations, or this sort of modular origami. It is nice and crisp, holds a fold really well, and doesn't crack. It comes in 70cm by 100cm sheets. I needed 360 squares, 120 of each color. I used a big straightedge and an xacto knife to cut the squares.
First I cut it into strips.
Then all the squares. The cutting actually took a long time because I wanted to be relatively accurate, so I only cut through one sheet at a time.
Now folding, first I did all the 'accordions'.
Then all the finished units! Two pictures for hours and hours of work spread out over several weeks.
Three units make a vertex like this. They slot together without any tape or glue which is nice.
Then a hexagon from 12 units.
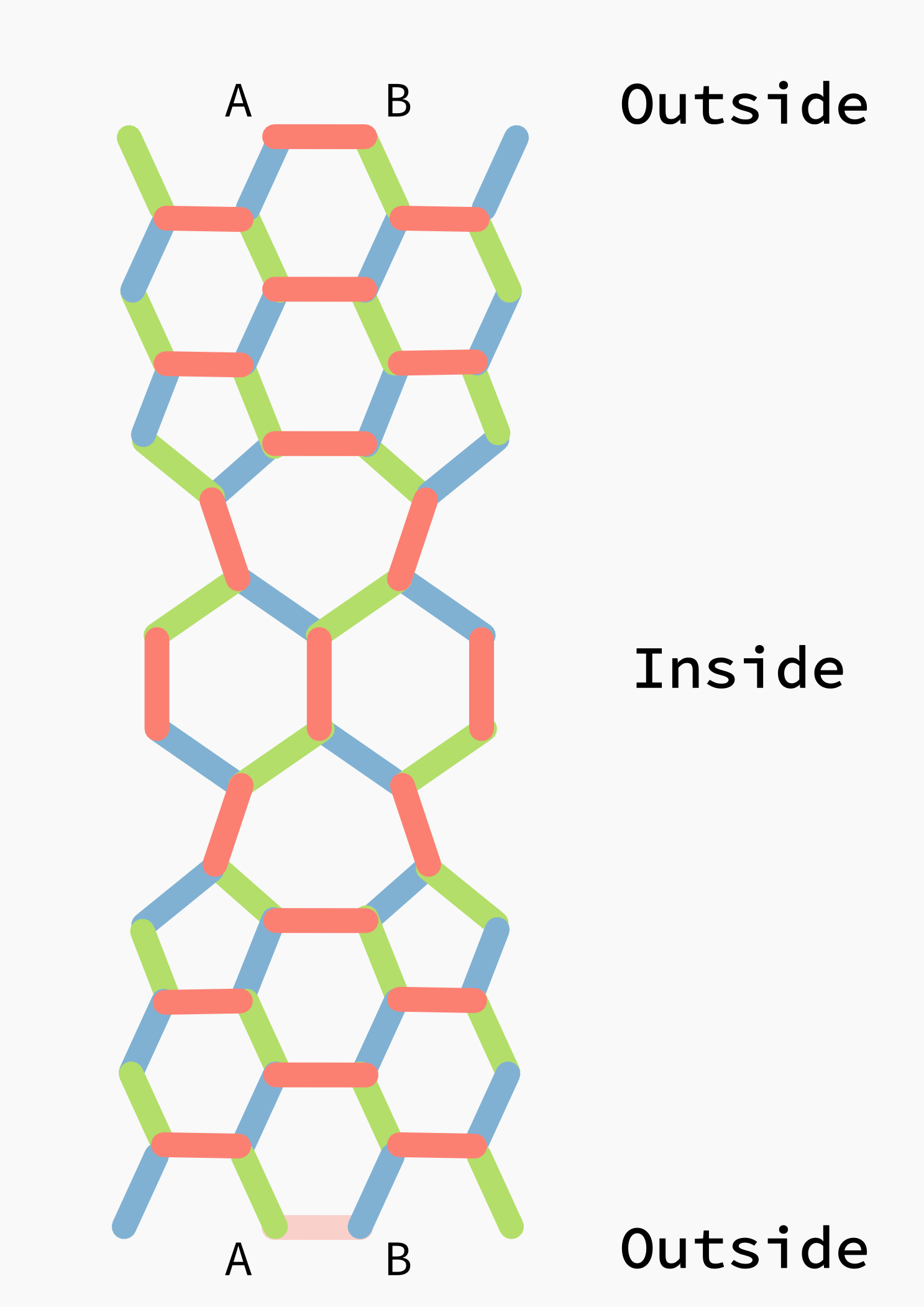
This is the only picture I have from the final assembly - got on a bit of a roll! I started with the inner 12 hexagons which was by far easiest, then all the heptagons, then the pentagons, and then finally all the remaining hexagons to close it out. You can follow this schematic for where the different polygons go, and what colors to use.
And here is the aforementioned schematic:
If you fold one, let me know!
Jiří Halamka sent me an email in June 2022 with a slightly improved schematic which I've linked here. I think his schematic more accurately represents the torus' 12 fold symmetry and is nicely numbered - this might be more clear to other's attempting to fold this torus. Thanks Jiří!
Diane completed the torus with a very pretty color scheme in March 2022:
Ant folded their torus with Christmas colors to serve as a very pretty wreath in December 2022:
Uli's rainbow torus cleanly demonstrates the twelve-fold symmetry. Completed in December 2022:
Sunil finished their torus in April of 2023 and described the process as "a blast!" I love the color scheme they chose:
Carissa made a very nice and fresh torus in November of 2023. They indicated that they folded the pieces during meetings - a great way to be doubly productive in my opinion! Additionally they created a schematic which shows all 360 pieces of the torus which might be useful for some. Linked here.
Omar made a small and colorful torus in January of 2024. One interesting choice they made was to create the PHiZZ units from 3x4 rectangles of paper - a neat idea, and potentially worth considering.
Origami_Zach made two tori in October of 2024 and posted them to reddit. They indicated that they are considering making several more which would be an impressive feat of patience. Well done!
matthewvdeutsch@gmail.com - © Matthew Deutsch. All rights reserved.
